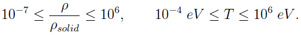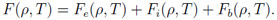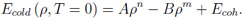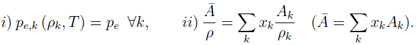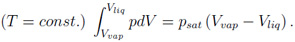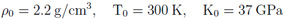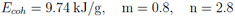|
||||||||
| Dr. Steffen Faik | ||||||||
|
FEOS ProgrammpaketDas FEOS (Frankfurt Equation-of-State) Programmpaket (früher bekannt unter dem Namen MPQeos-JWGU [1]) zur Berechnung und grafischen Darstellung von Zustandsgleichungen heißer, dichter Materie ist ein in C/C++ verfasster Computer-Code, der aus drei Teilen besteht:
Der dem FEOS Programmpaket zugrundeliegende Code MPQeos [3] basiert auf dem Zustandsgleichungsmodell QEOS [4] und wurde von A. Kemp et al. am Max-Planck-Institut für Quantenoptik in Garching bei München erstellt. Meine Motivation für die Weiterentwicklung war ein Teil meiner Diplomarbeit, der der Untersuchung metastabiler Zustände (überhitzter Flüssigkeiten) in volumetrisch erhitzter Materie (dünne Folien) [5] gewidmet war. Der originale MPQeos Code war in manchen Teilen nicht genau bzw. hinreichend genug für diese Untersuchung. Insbesondere benötigte ich die Zustandsgleichung für Element-Mischungen (Quarzglas bzw. Siliziumdioxid) und eine bessere Beschreibung der Flüssig-Gas-Koexistenz-Region. Mit den vorgenommenen Verbesserungen kann und soll der neue Code nun auch für andere Anwendungen bei der GSI in Darmstadt, insbesondere für strahlungshydrodynamische Simulationen benutzt werden. An dieser Stelle möchte ich Dr. Anna Tauschwitz, Prof. Dr. Joachim Maruhn (beide Goethe-Universität Frankfurt am Main & GSI Darmstadt), Prof. Dr. Igor Iosilevskiy (Joint Institute for High Temperatures Moscow & GSI Darmstadt) sowie Prof. Dr. Mikhail Basko (Institute for Theoretical and Experimental Physics Moscow & GSI Darmstadt) für sehr hilfreiche und konstruktive Diskussionen während der Entwicklung von FEOS danken. Beschreibung des QEOS-Modells und von MPQeos Die berechneten, thermodynamischen Zustandsgrößen sind: Druck, spezifische innere Energie, spezifische freie Energie, spezifische Entropie und Ladungszustand. Die Berechnungen können mit oder ohne Maxwell-Konstruktion, welche die van-der-Waals-Schleifen in der Flüssig-Gas-Koexistenz-Region eliminiert, durchgeführt werden. Die Eingabegrößen für die Zustandsgleichungsberechnung eines einzelnen Elements sind: Ordnungszahl, atomares Gewicht, Referenzbedingungen (Dichte und Temperatur, bei denen Druck und Energie auf Null gesetzt werden) und Kompressionsmodul unter den Referenzbedingungen. Der MPQeos Code wurde optimiert, um die Zustandsgleichung in dem folgenden Bereich zu berechnen:
Im QEOS-Modell werden alle thermodynamischen Größen aus der freien Energie abgeleitet. Diese setzt sich aus drei Anteilen - dem (unkorrigierten) Elektronen-, dem Ionenanteil und der sogenannten Bindungskorrektur - zusammen:
Die Berechnung des Elektronen-Anteils erfolgt unter Zuhilfename des simplen Thomas-Fermi (TF) - Modells [6]. Die Elektronen werden als Fermi-Gas im selbst-konsistenten elektrostatischen Feld des Atoms beschrieben. Die Materie wird in sphärische Zellen unterteilt. Für diese wird die Gleichgewichtselektronenverteilung durch Lösen der TF-Gleichung berechnet. Berechnungen mit dem einfachen TF-Modell sind viel schneller als mit erweiterten TF-Theorien, weil alle thermodynamischen Größen mit der Ordnungszahl skalieren und daher nur einmalig, z.B. für Wasserstoff, berechnet werden müssen. Die beiden größten Nachteile des simplen TF-Modells sind die Überschätzung des Drucks und der Temperatur des kritischen Punktes sowie die Überschätzung der Drücke nahe der Festkörperdichte. Der Grund für diese beiden Defizite ist die Vernachlässigung anziehender, bindender Kräften zwischen neutralen Atomen in der einfachen TF-Theorie. Die sogenannte Bindungskorrektur [7], der Rekalibrierungspart von QEOS, wird zur gesamten Zustandsgleichung (bzw. zum Elektronanteil) addiert, um die eben genannten Defizite des Elektronenanteils zu beseitigen. Sie justiert die Zustandsgleichung zu verschwindendem Druck / Energie und zum eingegebenen Kompressionsmodul (und damit auch zur Schallgeschwindigkeit) unter Referenzbedingungen. Der Ionen-Anteil wird mit dem Cowan-Modell berechnet. Hierbei handelt es sich um ein semi-empirisches Modell, welches zwischen bekannten physikalischen Gesetzen (z.B. dem idealen Gas-Gesetz und dem Dulong-Petit-Gesetz) interpoliert. Da kein Volumensprung beim Schmelzpunkt vorhanden ist, ist der Vorgang des Schmelzens im QEOS-Modell nicht enthalten. Verbesserungen an der kalten Kurve Trotz der Existenz der Bindungskorrektur überschätzt das QEOS-Modell immer noch die Lage des kritischen Punktes (Druck und Temperatur). Außerdem kann es in einigen wenigen Fällen dazu kommen, dass die Sublimationswärme - auch als kohäsive Energie bezeichnet - negativ wird. Um dieses Problem zu lösen, habe ich die TF-Kalte-Kurve und die Bindungskorrektur für Dichten unterhalb der Referenzdichte durch eine von Young et al. [8] vorgeschlagene Soft-Sphere-Funktion ersetzt:
Die Konstanten A und B werden derart angepasst, dass der Druck und die innere Energie der gesamten Zustandsgleichung bei Referenzbedingungen verschwinden; m und n sind freie Parameter. Sie werden justiert, um sich dem experimentell oder theoretisch ermittelten kritischen Punkt anzunähern. Die folgende Auflistung zeigt wie die Soft-Sphere-Funktion die Lage des kritischen Punktes von Aluminium beeinflusst:
Die Nachteile dieser neuen, einfachen Form der kalten Kurve sind auf der einen Seite ein Fehlen an Flexibilität mit nur zwei freien Parametern. Auf der anderen Seite kann die Schallgeschwindigkeit bei der Referenzdichte unstetig werden. Berechnung von Mischungen von Elementen In der MPQeos-Version, die mir zur Verfügung gestellt wurde, gab es keine Möglichkeit, die Zustandsgleichung von Mischungen von Elementen zu berechnen. Daher fügte ich die so genannte TF-Element-Mischungsmethode, welche in der QEOS-Beschreibung [4] erläutert wird, zur FEOS Programmbibliothek hinzu. Der Ionenanteil und die Bindungskorrektur werden wie ein einzelnes Element mit gemittelter Ordnungszahl Z und gemitteltem atomaren Gewicht A behandelt. Für den Elektronen-Anteil der Mischung werden die Dichten (effektiv die Partialvolumina) von allen Spezies iterativ derart ermittelt, dass alle TF-Drücke gleich sind und ein additives Volumen-Gesetz erfüllt ist:
Hierbei ist xk der zahlenmäßige Anteil und Ak das atomare Gewicht von Spezies k. Die thermodynamischen Zustandsgrößen der Elektronen-Komponente der Mischung erhält man schließlich, indem die Werte der einzelnen Elemente (berechnet mit den zuvor durch das beschriebene Schema erhaltenen Dichten) gewichtet durch xk Ak / A summiert werden. Da die beschriebene Prozedur für jeden Dichte-Temperatur-Punkt aufgerufen wird, ist es leicht einzusehen, dass die Berechnung von Element-Mischungen rechenintensiver ist als für ein einzelnes Element. Behandlung der Flüssig-Gas-Phasen-Koexistenz Im Original-Quellcode von MPQeos wird die Phasen-Koexistenz für jede Isotherme unterhalb der kritischen Temperatur mit Hilfe von Maxwells geometrischer Regel der gleichen Flächen ober- und unterhalb der van-der-Waals-Schleifen behandelt:
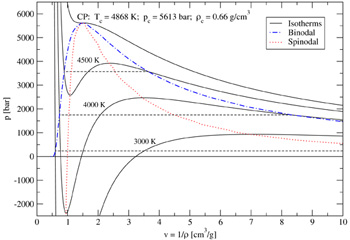
Maxwells Regel ist insbesondere für niedrige Temperaturen innerhalb der Zwei-Phasen-Region sehr rechenintensiv und unpräzise. Ich habe dieses Problem gelöst, indem ich eine neue Routine für die Behandlung der Phasen-Koexistenz geschrieben habe. Die Koexistenz-Begrenzung - auch die Binodale genannt - und der Gleichgewichts- bzw. Sättigungsdampfdruck werden unter Berücksichtigung des Gleichgewichts der freien Enthalpien und Drücke auf der flüssigen und der gasförmigen Seite für jede Isotherme unterhalb der kritischen Temperatur berechnet. Dies führt zu einer spürbaren Verbesserung in der Rechenzeit und der Genauigkeit der Berechnung. Beispiel: Berechnung der Phasen-Koexistenz-Kenngrößen für SiO2
Verfügbarkeit des Programms Der Code wurde zusammen mit dem Artikel [9] "The equation of state package FEOS for high energy density matter" in Computer Physics Communications veröffentlicht: Computer Physics Communications 227 (2018) 117–125, https://doi.org/10.1016/j.cpc.2018.01.008. Literatur [1] S. Faik, An. Tauschwitz, J. Maruhn, I. Iosilevskiy; GSI Darmstadt; Report 2012-1, PNI-PP-12; [2] T. Group; Report No. LALP-83-4, Los Alamos National Laboratory (1983); [3] A. Kemp, J. Meyer-ter-Vehn, Nucl. Instrum. Methods A 415 (1998) 674; [4] R. More, K. Warren, D. Young, G. Zimmerman; Phys. Fluids 31 (1988) 3059; [5] S. Faik, M. Basko, An. Tauschwitz, I. Iosilevskiy, J. Maruhn; HEDP 8 (2012) 349-359; [6] L. Thomas; Proc. Camb. Phil. Soc 23 (1927) 542; E. Fermi; Zeitschrift für Physik 48 (1928) 73; [7] J. Barnes; Physical Review 153 (1967); [8] D. Young, E.M. Corey; J. Appl. Phy. 6 (1995) 3748; [9] S. Faik, An. Tauschwitz, I. Iosilevskiy; CPC 227 (2018) 117–125. |
||||||||||||||
| Letzte Aktualisierung: 15.04.2021 |
 English
English